[Calculus] Logistic Growth
By: Tao Steven Zheng (鄭濤)
【Problem】
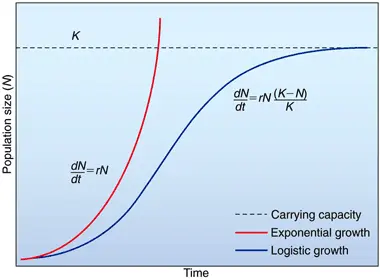
The logistic growth model is a population model that incorporates Malthusian-like growth in the early stage and in-species competition for resources at the later stage. This model includes a growth rate and carrying capacity
. The differential equation of this growth model is
with the initial condition .
Part 1: What are the steady-state solutions?
Part 2: Solve the differential equation with the aforementioned initial condition.

【Solution】
Part 1
Steady-state solutions occur when for all time
. For the logistic growth model,
Solving for shows that the steady-state solutions occur at
and
.
Part 2
Rewrite the differential equation as
.
Integrate both sides
by partial fractions using the fact
Consequently,
Let , then
Solve the initial-value problem:
Consequently, the solution of the logistic growth model is

