BST reports the k smallest elements of S in O(k) time
Sure, I'd be happy to explain the algorithm for reporting the k smallest elements of S in O(k) time, for any k satisfying 1 ≤ k ≤ n.
The idea behind the algorithm is to perform an in-order traversal of the binary search tree in order to visit its elements in ascending order. During the traversal, we maintain a count of the number of elements visited so far, and we stop the traversal as soon as we have visited k elements.
Here's the step-by-step algorithm:
Initialize an empty stack S and a counter count to 0.
Push the root of the binary search tree onto S.
While S is not empty and count < k: a. Pop the top element from S and call it node. b. If node has a left child, push the left child onto S. c. If node has a right child, push the right child onto S. d. Increment count by 1.
Return the k smallest elements that have been visited during the traversal.
Let's walk through an example to see how this algorithm works. Consider the following binary search tree:
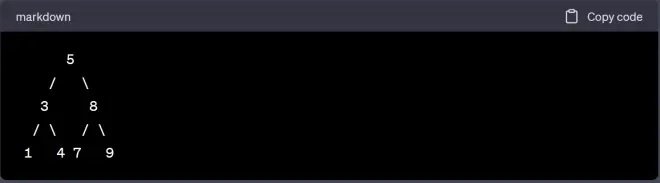
Suppose we want to report the 3 smallest elements of this tree. Here's how the algorithm would execute:
Initialize an empty stack S and a counter count to 0.
Push the root (5) onto S.
S contains [5]. count = 0 < k = 3. a. Pop 5 from S and call it node. b. Push node's left child (3) onto S. S contains [3]. c. Push node's right child (8) onto S. S contains [3, 8]. d. Increment count to 1.
S contains [3, 8]. count = 1 < k = 3. a. Pop 8 from S and call it node. b. Push node's left child (7) onto S. S contains [3, 7]. c. Push node's right child (9) onto S. S contains [3, 7, 9]. d. Increment count to 2.
S contains [3, 7, 9]. count = 2 < k = 3. a. Pop 9 from S and call it node. b. Since node has no left or right child, do nothing. c. Increment count to 3.
We have visited k = 3 elements, so we stop the traversal and return the 3 smallest elements visited during the traversal, which are [1, 3, 4].
Since the traversal visits each element in the tree once, and we only visit k elements, the time complexity of this algorithm is O(k).