Reinforcement Learning_Code_Dynamic Programming
CliffWalkingEnv.py
import numpy as np
class CliffWalkingEnv:
? ?'''
? ?Environment of cliff walking problem.
? ?P[state][action] = [(p_rsa, reward, next_state)]
? ? ? ?p_rsa: p(reward|state, action).
? ?'''
? ?def __init__(self, nrow = 4, ncol = 12):
? ? ? ?self.nrow = nrow
? ? ? ?self.ncol = ncol
? ? ? ?self.action_space = [[-1, 0], [0, 1], [1, 0], [0, -1], [0, 0]]
? ? ? ?self.P = self.createP()
? ? ? ?
? ?def createP(self):
? ? ? ?P = [[[] for actions_number in np.arange(len(self.action_space))]
? ? ? ? ? ? for states_number in np.arange(self.nrow * self.ncol)]
? ? ? ?for i in np.arange(self.nrow):
? ? ? ? ? ?for j in np.arange(self.ncol):
? ? ? ? ? ? ? ?now_state = i * self.ncol + j
? ? ? ? ? ? ? ?reward = 0
? ? ? ? ? ? ? ?if i == self.nrow - 1:
? ? ? ? ? ? ? ? ? ?if j == self.ncol - 1:
? ? ? ? ? ? ? ? ? ? ? ?reward = 1
? ? ? ? ? ? ? ? ? ?elif j > 0:
? ? ? ? ? ? ? ? ? ? ? ?reward = -100
? ? ? ? ? ? ? ?for action_index in np.arange(len(self.action_space)):
? ? ? ? ? ? ? ? ? ?next_i = max(0, min(self.nrow - 1,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?i + self.action_space[action_index][0]))
? ? ? ? ? ? ? ? ? ?next_j = max(0, min(self.ncol - 1,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?j + self.action_space[action_index][1]))
? ? ? ? ? ? ? ? ? ?next_state = next_i * self.ncol + next_j
? ? ? ? ? ? ? ? ? ?P[now_state][action_index] = [(1, reward, next_state)]
? ? ? ?return PPolicyIteration.py
import numpy as np
import copy
class PolicyIteration:
? ?'''
? ?Policy iteration algorithm.
? ?Input:
? ? ? ?env: Environment of the problem.
? ? ? ?gamma: Discount.
? ? ? ?theta: Convergence threshold.
? ?Member:
? ? ? ?self.v[s]: State value function of state s.
? ? ? ? ? ? ? ? ? An initial guess filled with zero is given.
? ? ? ?self.pi[s][a]: Policy of (state s, action a).
? ?'''
? ?def __init__(self, env, gamma = 0.9, theta = 1e-3):
? ? ? ?self.env = env
? ? ? ?self.v = [0] * self.env.nrow * self.env.ncol
? ? ? ?self.pi = [[1.0/len(self.env.action_space)
? ? ? ? ? ? ? ? ? ?for action_idx in np.arange(len(self.env.action_space))]
? ? ? ? ? ? ? ? ? for states_number in np.arange(self.env.nrow * self.env.ncol)]
? ? ? ?self.gamma = gamma
? ? ? ?self.theta = theta
? ?def policy_evaluation(self):
? ? ? ?'''
? ? ? ?Calculates state value for all states under current policy and updates
? ? ? ?self.v.
? ? ? ?Input:
? ? ? ? ? ?None.
? ? ? ?Output:
? ? ? ? ? ?None.
? ? ? ?max_delta: Maximum difference between old state value
? ? ? ? ? ? ? ? ? and new state value.
? ? ? ?new_v[s]: State value of state s under current policy.
? ? ? ?old_q[a]: Action value of (fixed state s, action a) under old policy.
? ? ? ?'''
? ? ? ?iteration = 0
? ? ? ?while True:
? ? ? ? ? ?iteration += 1
? ? ? ? ? ?max_delta = 0
? ? ? ? ? ?new_v = [0 for i in np.arange(self.env.nrow * self.env.ncol)]
? ? ? ? ? ?for state in np.arange(self.env.nrow * self.env.ncol):
? ? ? ? ? ? ? ?old_q = [0 for i in np.arange(len(self.env.action_space))]
? ? ? ? ? ? ? ?for action_index in np.arange(len(self.env.action_space)):
? ? ? ? ? ? ? ? ? ?for p_rsa, reward, next_state in \
? ? ? ? ? ? ? ? ? ? ? ?self.env.P[state][action_index]:
? ? ? ? ? ? ? ? ? ? ? ?old_q[action_index] += (p_rsa * reward
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?+ self.gamma * self.v[next_state])
? ? ? ? ? ? ? ? ? ?old_q[action_index] *= self.pi[state][action_index]
? ? ? ? ? ? ? ?new_v[state] = sum(old_q)
? ? ? ? ? ? ? ?max_delta = max(max_delta, abs(new_v[state] - self.v[state]))
? ? ? ? ? ?self.v = new_v
? ? ? ? ? ?if max_delta < self.theta:
? ? ? ? ? ? ? ?break
? ? ? ?print("Policy evaluation is done after %d iterations." % (iteration))
? ?def policy_improvement(self):
? ? ? ?'''
? ? ? ?Improve the policy at every state s.
? ? ? ?Input:
? ? ? ? ? ?None.
? ? ? ?Output:
? ? ? ? ? ?The updated policy.
? ? ? ?new_q[a]: Action value of (fixed state s, action a) under new policy.
? ? ? ?optimal_q: Optimal action value.
? ? ? ?count_optimality: Number of actions with optimal action value.
? ? ? ?'''
? ? ? ?for state in np.arange(self.env.nrow * self.env.ncol):
? ? ? ? ? ?new_q = [0] * len(self.env.action_space)
? ? ? ? ? ?for action_idx in np.arange(len(self.env.action_space)):
? ? ? ? ? ? ? ?for p_rsa, reward, next_state \
? ? ? ? ? ? ? ? ? ?in self.env.P[state][action_idx]:
? ? ? ? ? ? ? ? ? ?new_q[action_idx] += (p_rsa * reward
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?+ self.gamma * self.v[next_state])
? ? ? ? ? ?optimal_q = max(new_q)
? ? ? ? ? ?count_optimality = new_q.count(optimal_q)
? ? ? ? ? ?self.pi[state] = \
? ? ? ? ? ? ? ?([1.0/count_optimality
? ? ? ? ? ? ? ? ?if (new_q[action_idx] == optimal_q) else 0
? ? ? ? ? ? ? ? ?for action_idx in np.arange(len(self.env.action_space))])
? ? ? ?print("Policy improvement is done.")
? ? ? ?return self.pi
? ?def policy_iteration(self):
? ? ? ?'''
? ? ? ?Iteratively perform policy evaluation and policy improvement until the
? ? ? ?policy converges.
? ? ? ?old_policy: Policy before improvement.
? ? ? ?new_policy: Policy after improvement.
? ? ? ?'''
? ? ? ?while True:
? ? ? ? ? ?self.policy_evaluation()
? ? ? ? ? ?old_policy = copy.deepcopy(self.pi)
? ? ? ? ? ?new_policy = self.policy_improvement()
? ? ? ? ? ?if old_policy == new_policy:
? ? ? ? ? ? ? ?breakValueIteration.py
import numpy as np
class ValueIteration:
? ?'''
? ?Value iteration algorithm
? ?Member:
? ? ? ?env: The environment of the problem.
? ? ? ?gamma: Discount
? ? ? ?theta: Convergence threshold.
? ? ? ?v[s]: State value of state s. A zero initial guess is given.
? ? ? ?pi[s][a]: Action value of (state s, action a).
? ? ? ? ? ? ? ? ?An average initial guess is given.
? ?'''
? ?def __init__(self, env, gamma = 0.9, theta = 1e-3):
? ? ? ?self.env = env
? ? ? ?self.gamma = gamma
? ? ? ?self.theta = theta
? ? ? ?self.v = [0 for state in np.arange(self.env.nrow * self.env.ncol)]
? ? ? ?self.pi = [[1.0/len(self.env.action_space)
? ? ? ? ? ? ? ? ? ?for action in self.env.action_space]
? ? ? ? ? ? ? ? ? for state in np.arange(self.env.nrow * self.env.ncol)]
? ?def policy_value_update(self):
? ? ? ?'''
? ? ? ?Perform policy update and value update.
? ? ? ?Input:
? ? ? ? ? ?None.
? ? ? ?Output:
? ? ? ? ? ?Updated policy.
? ? ? ?new_v[s]: Intermediate value of state s.(Not state value.)
? ? ? ?q[a]: Intermediate value of (fixed state s, action a).
? ? ? ? ? ? ?(Not action value.)
? ? ? ?max_delta: maximum difference between old v[s] and new v[s]
? ? ? ?'''
? ? ? ?iteration = 0
? ? ? ?while True:
? ? ? ? ? ?iteration += 1
? ? ? ? ? ?max_delta = 0
? ? ? ? ? ?new_v = [0 for state in np.arange(self.env.nrow * self.env.ncol)]
? ? ? ? ? ?for state in np.arange(self.env.nrow * self.env.ncol):
? ? ? ? ? ? ? ?q = [0 for action in self.env.action_space]
? ? ? ? ? ? ? ?for action_index in np.arange(len(self.env.action_space)):
? ? ? ? ? ? ? ? ? ?for p_rsa, reward, next_state in \
? ? ? ? ? ? ? ? ? ? ? ?self.env.P[state][action_index]:
? ? ? ? ? ? ? ? ? ? ? ?q[action_index] = (p_rsa * reward
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? + self.gamma * self.v[next_state])
? ? ? ? ? ? ? ?optimal_action_index = q.index(max(q))
? ? ? ? ? ? ? ?self.pi[state] = [1.0 if (action_index
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?== optimal_action_index) else 0
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?for action_index in \
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?np.arange(len(self.env.action_space))]
? ? ? ? ? ? ? ?new_v[state] = q[optimal_action_index]
? ? ? ? ? ? ? ?max_delta = max(max_delta, abs(new_v[state] - self.v[state]))
? ? ? ? ? ?self.v = new_v
? ? ? ? ? ?if max_delta < self.theta:
? ? ? ? ? ? ? ?print("Policy update and value update is done", end = '')
? ? ? ? ? ? ? ?print("after %d iterations." % iteration)
? ? ? ? ? ? ? ?break
? ? ? ?returnTruncatedPolicyIteration.py
import numpy as np
import copy
class TruncatedPolicyIteration:
? ?'''
? ?Truncated Policy iteration algorithm.
? ?Input:
? ? ? ?env: Environment of the problem.
? ? ? ?gamma: Discount.
? ? ? ?theta: Convergence threshold.
? ? ? ?truncate_iteration: maximum iteration in policy evaluation.
? ?Member:
? ? ? ?self.v[s]: Intermediate state value of state s. (Not real state value.)
? ? ? ? ? ? ? ? ? An initial guess filled with zero is given.
? ? ? ?self.pi[s][a]: Intermediate policy of (state s, action a).
? ? ? ? ? ? ? ? ? ? ? ?(Not real policy.)
? ?'''
? ?def __init__(self, env, gamma = 0.9, theta = 1e-3, truncate_iteration = 10):
? ? ? ?self.env = env
? ? ? ?self.v = [0] * self.env.nrow * self.env.ncol
? ? ? ?self.pi = [[1.0/len(self.env.action_space)
? ? ? ? ? ? ? ? ? ?for action_idx in np.arange(len(self.env.action_space))]
? ? ? ? ? ? ? ? ? for states_number in np.arange(self.env.nrow * self.env.ncol)]
? ? ? ?self.gamma = gamma
? ? ? ?self.theta = theta
? ? ? ?self.truncate_iteration = truncate_iteration
? ?def policy_evaluation(self):
? ? ? ?'''
? ? ? ?Calculates state value for all states under current policy and updates
? ? ? ?self.v.
? ? ? ?Input:
? ? ? ? ? ?None.
? ? ? ?Output:
? ? ? ? ? ?None.
? ? ? ?max_delta: Maximum difference between old state value
? ? ? ? ? ? ? ? ? and new state value.
? ? ? ?new_v[s]: Intermediate state value of state s under current policy.
? ? ? ? ? ? ? ? ?(Not real state value.)
? ? ? ?old_q[a]: Intermediate action value of (fixed state s, action a) under
? ? ? ? ? ? ? ? ?old policy. (Not real action value.)
? ? ? ?'''
? ? ? ?iteration = 0
? ? ? ?while iteration < self.truncate_iteration:
? ? ? ? ? ?iteration += 1
? ? ? ? ? ?max_delta = 0
? ? ? ? ? ?new_v = [0 for i in np.arange(self.env.nrow * self.env.ncol)]
? ? ? ? ? ?for state in np.arange(self.env.nrow * self.env.ncol):
? ? ? ? ? ? ? ?old_q = [0 for i in np.arange(len(self.env.action_space))]
? ? ? ? ? ? ? ?for action_index in np.arange(len(self.env.action_space)):
? ? ? ? ? ? ? ? ? ?for p_rsa, reward, next_state in \
? ? ? ? ? ? ? ? ? ? ? ?self.env.P[state][action_index]:
? ? ? ? ? ? ? ? ? ? ? ?old_q[action_index] += (p_rsa * reward
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?+ self.gamma * self.v[next_state])
? ? ? ? ? ? ? ? ? ?old_q[action_index] *= self.pi[state][action_index]
? ? ? ? ? ? ? ?new_v[state] = sum(old_q)
? ? ? ? ? ? ? ?max_delta = max(max_delta, abs(new_v[state] - self.v[state]))
? ? ? ? ? ?self.v = new_v
? ? ? ? ? ?if max_delta < self.theta:
? ? ? ? ? ? ? ?break
? ? ? ?print("Policy evaluation is done after %d iterations." % (iteration))
? ?def policy_improvement(self):
? ? ? ?'''
? ? ? ?Improve the policy at every state s.
? ? ? ?Input:
? ? ? ? ? ?None.
? ? ? ?Output:
? ? ? ? ? ?The updated policy.
? ? ? ?new_q[a]: Action value of (fixed state s, action a) under new policy.
? ? ? ?optimal_q: Optimal action value.
? ? ? ?count_optimality: Number of actions with optimal action value.
? ? ? ?'''
? ? ? ?for state in np.arange(self.env.nrow * self.env.ncol):
? ? ? ? ? ?new_q = [0] * len(self.env.action_space)
? ? ? ? ? ?for action_idx in np.arange(len(self.env.action_space)):
? ? ? ? ? ? ? ?for p_rsa, reward, next_state \
? ? ? ? ? ? ? ? ? ?in self.env.P[state][action_idx]:
? ? ? ? ? ? ? ? ? ?new_q[action_idx] += (p_rsa * reward
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?+ self.gamma * self.v[next_state])
? ? ? ? ? ?optimal_q = max(new_q)
? ? ? ? ? ?count_optimality = new_q.count(optimal_q)
? ? ? ? ? ?self.pi[state] = \
? ? ? ? ? ? ? ?([1.0/count_optimality
? ? ? ? ? ? ? ? ?if (new_q[action_idx] == optimal_q) else 0
? ? ? ? ? ? ? ? ?for action_idx in np.arange(len(self.env.action_space))])
? ? ? ?print("Policy improvement is done.")
? ? ? ?return self.pi
? ?def policy_iteration(self):
? ? ? ?'''
? ? ? ?Iteratively perform policy evaluation and policy improvement until the
? ? ? ?policy converges.
? ? ? ?old_policy: Policy before improvement.
? ? ? ?new_policy: Policy after improvement.
? ? ? ?'''
? ? ? ?while True:
? ? ? ? ? ?self.policy_evaluation()
? ? ? ? ? ?old_policy = copy.deepcopy(self.pi)
? ? ? ? ? ?new_policy = self.policy_improvement()
? ? ? ? ? ?if old_policy == new_policy:
? ? ? ? ? ? ? ?breakdynamic_programming.py
from CliffWalkingEnv import CliffWalkingEnv
from PolicyIteration import PolicyIteration
from ValueIteration import ValueIteration
from TruncatedPolicyIteration import TruncatedPolicyIteration
import time
def print_agent(agent, action_meaning):
? ?print("State value function")
? ?for i in range(agent.env.nrow):
? ? ? ?for j in range(agent.env.ncol):
? ? ? ? ? ?print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')
? ? ? ?print()
? ?print("Policy: ")
? ?for i in range(agent.env.nrow):
? ? ? ?for j in range(agent.env.ncol):
? ? ? ? ? ?actions = agent.pi[i * agent.env.ncol + j]
? ? ? ? ? ?optimal_action_index = actions.index(max(actions))
? ? ? ? ? ?print('%3s' % (action_meaning[optimal_action_index]), end = ' ')
? ? ? ?print()
if __name__ == '__main__':
? ?env = CliffWalkingEnv()
? ?action_meaning = ['^', '>', 'v', '<', 'o']
? ?gamma = 0.9
? ?theta = 1e-3
? ?truncated_iteration = 100
? ?start_time = time.time()
? ?'''Perform dynamic programming by policy iteration'''
? ?#agent = PolicyIteration(env, gamma, theta)
? ?#agent.policy_iteration()
? ?'''Perform dynamic programming by value iteration'''
? ?#agent = ValueIteration(env, gamma, theta)
? ?#agent.policy_value_update()
? ?'''Perform dynamic programming by truncated policy iteration'''
? ?agent = TruncatedPolicyIteration(env, gamma, theta, truncated_iteration)
? ?agent.policy_iteration()
? ?end_time = time.time()
? ?print_agent(agent, action_meaning)
? ?print("Time cost: %.3f s." % (end_time - start_time))Results of policy iteratoin, value iteration and truncated policy iteration with iteration of 1, 10 and 100 are respectively shown below.
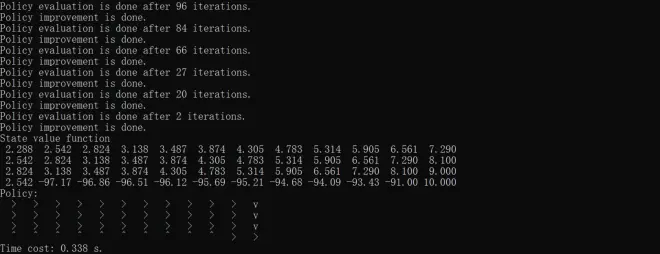
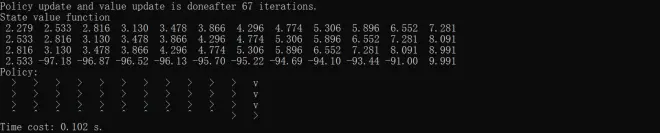
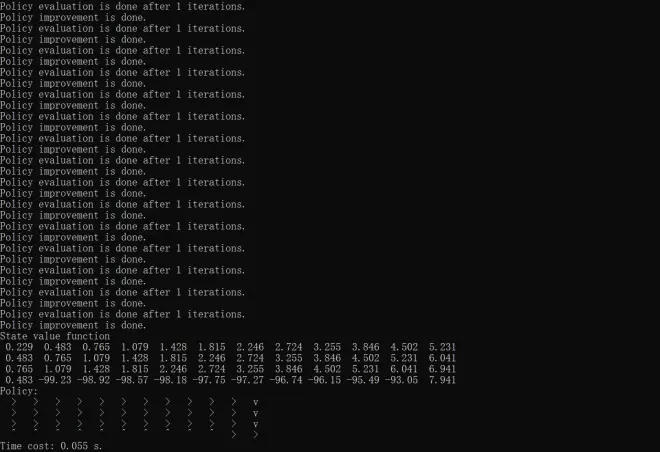
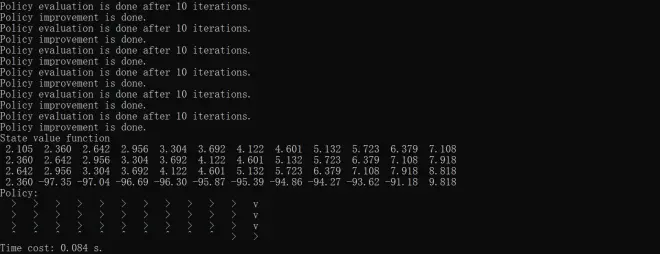
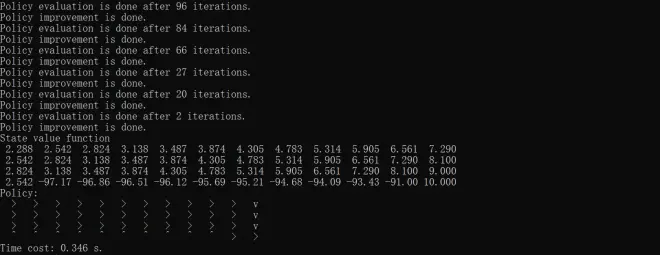
The above codes mainly refer to Chapter 4 of?Hands-on Reinforcement Learning, but some changes have been made?based on?David Silver's lecture and?Shiyu Zhao's?Mathematical Foundation of Reinforcement Learning.
[1]?https://hrl.boyuai.com/
[2] https://www.davidsilver.uk/teaching/
[3] https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning
標(biāo)簽:

