Size of Singularity of Minimal Surfaces - Camillo De Lellis

The talk is about the regularity problem of Plateau's problem for any dimension and codimensions. This is the Joint work of De Lellis and Spadaro (We focus on Federer and Fleming's theory of integral rectifiable currents in this talk (This is the generalization of De Giorgi's theory of Caccioppoli set which works in codimension 1))

Briefly introduce currents:

Here is a nice explanation by De Lellis on the volume of the currents (in the case of codim = 1): Take the integral over the vector fields with modules less than or equal to 1 times the unit normal vector field.

This allows us to apply the theorem to linear functional analysis. But the solution might not be classical surfaces.

The currents T here is a solution, but far from being a single surface. Then Federer and Fleming in 60 defined a more restricted family of generalization of surfaces called integer rectifiable currents

The existence theorem is still correct if we restrict our class of surfaces from currents to integer rectifiable currents. This existence theorem is much harder than the version for currents because integer rectifiable currents have no linear structure, so we cannot apply classical functional analysis to show the existence of the solution to the Plateau problem. However, this theorem can be proved using the deformation lemma (very technical, but provide a nice approximation property) in geometric measure theory.

Now, we start talking about some regularity results.

The manuscript was made by Almgren. De Lellis said even Pitts doesn’t understand the proof. (這里沒聽清, 好像說(shuō)Pitts也不懂)

這里De Lellis說(shuō)證明Holomorphic su bvarieties are area minimizing currents不是特別難.

Indeed, the regularity is very hard in codimension higher than 1, because it is easier to give counterexamples.

Here are two typical examples of singularity in C^2 we need to keep in mind, at 0 no way to write the subvarieties a graph of a smooth function.

Introduction to the joint work of De Lellis and Spadaro: but

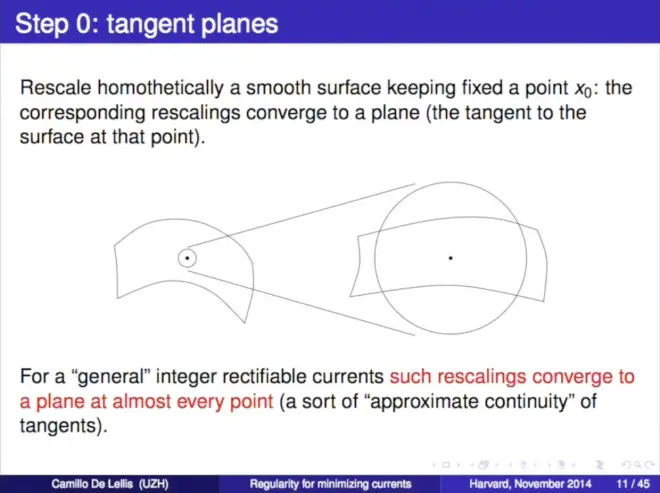
The important point here is that the integral quantity of the gradient or higher order derivatives has excess decay property, which is important in elliptic regularity theory (could upgrade by a compactness argument that the decay of this integral quantity to the solution of the nonlinear problem). Once we have this decay, we can obtain some continuity result of something. In this talk, we focus on the harmonic case

De Lellis said the quantity here is incorrect, it should be more complicated

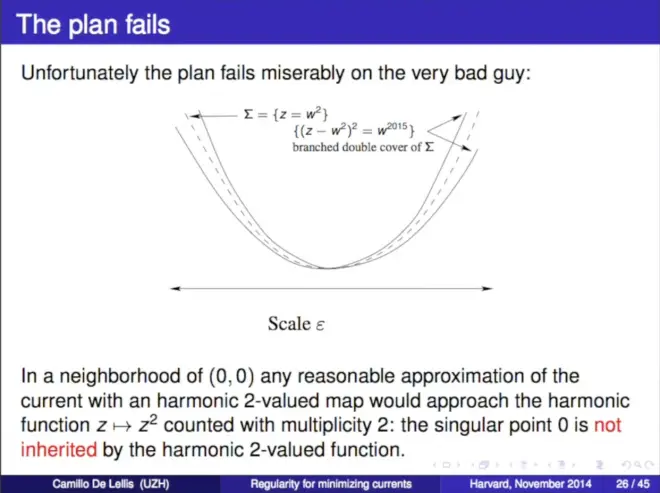
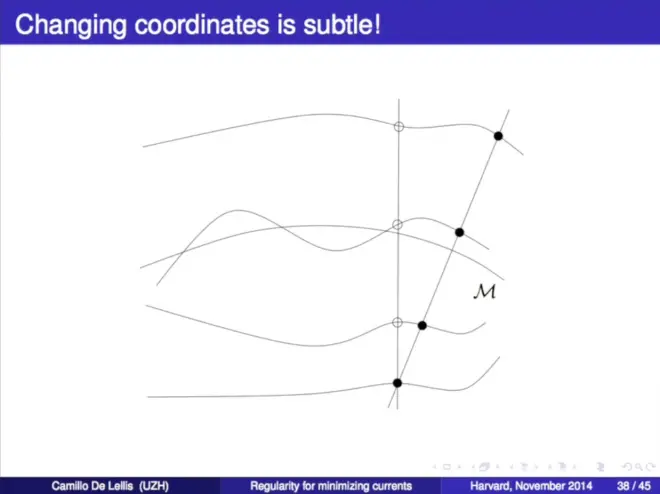
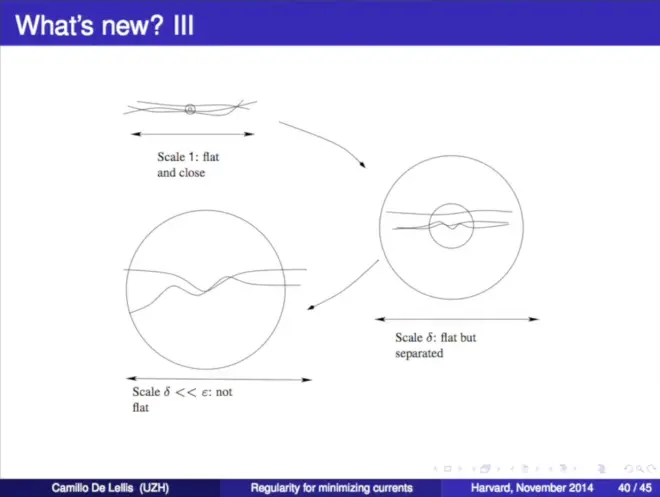
(Combinatorial Problem Here)