[Number Theory] Dayan Method
By: Tao Steven Zheng (鄭濤)
The following number theory problem is from the ''Shushu Jiuzhang'' (數(shù)書九章) by Qin Jiushao (秦九韶, 1202 - 1261 AD). The solution presented here outlines Qin Jiushao's version of the Euclidean algorithm (大衍求一術(shù) ''dayan qiuyi shu'') and his generalized Chinese Remainder Theorem (大衍總數(shù)術(shù) ''dayan zongshu shu'').

【Problem】
There are three farmers of the highest class. As for the grain they harvested from their fields, when making use of a full standard ''dou'', the amounts are the same. All of them go to different places to sell their grain. After selling his grain on the official markets of his own prefecture, A has 3 ''dou'' 2 ''sheng'' remaining. After selling his grain to the villagers of Anji, B has 7 ''dou'' remaining. After selling his grain to an agent from Pingjiang, C has 3 ''dou'' remaining. How much grain did the farmers have altogether, and how much did each farmer sell in terms of the respective capacity rates in ''dan''?
In the solution, Qin Jiushao reveals that each market has a different unit of volume called ''hu'' (斛): the official market ''hu'' is 8 ''dou'' 3 ''sheng'', the Anji ''hu'' is 1 ''dan'' 1 ''dou'', and the Pingjiang ''hu'' is 1 ''dan'' 3 ''dou'' 5 ''sheng''.
Since 1 ''dan'' = 10 ''dou'' = 100 ''sheng'' and 1 ''dou'' = 10 ''sheng'', this problem is a system of modular congruences:
Calculate the lowest positive integer solution.

【Solution】
Part 1: Determine the ''dingshu'' 求定數(shù)
The initial problem begins with the moduli, which Qin Jiushao called ''wenshu'' (問(wèn)數(shù)), are . Since the moduli are natural numbers, they are referred to as ''yuanshu'' (元數(shù)) and the remainders
.
Notice that the second and third moduli are not coprime because 110 and 135 share a common divisor 5. This is determined by an often lengthy procedure called the ''lianhuan qiudeng'' (連環(huán)求等). Qin Jiushao’s algorithm prescribes that the congruence of odd moduli be reduced, which in this case is the third moduli. The new moduli, called ''dingshu'' (定數(shù)), are . Because
, the new remainder of the third congruence is 3. Hence, the new remainders are
.
Subsequently, the new problem with coprime moduli to solve is:
Part 2: Determine the ''yanmu'' and the ''yanshu'' 求衍母和衍數(shù)
First calculate the ''yanmu'' (衍母) , which is the product of the coprime moduli.
Divide the ''yanmu''(衍母) by each moduli to obtain each ''yanshu''(衍數(shù)) .
Part 3: Determine the ''chenglü'' 求乘率
The next step is to determine the ''qishu'' (奇數(shù)) , which satisfies
.
Next solve each congruence , where
is called the ''chenglü'' (乘率). Qin Jiushao solves each congruence with what he calls the ''dayan qiuyi shu'' (大衍求一術(shù)), which is the Euclidean algorithm.

Here we will demonstrate how the ''dayan qiuyi shu'' works for .
Step 1: Set up the ''tianyuan'' (天元), ''qishu'' (奇數(shù)), and ''dingshu'' (定數(shù)).

Step 2: Perform the calculations and sequencing of the ''dayan qiuyi shu''.
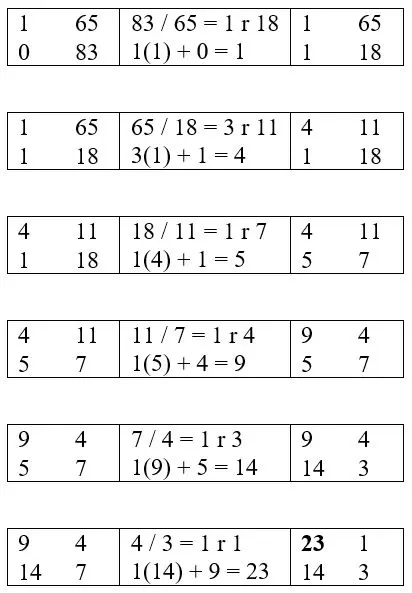
The solution for this system is .
Part 4: Determine the ''yongshu'' and the ''zongshu'' 求用數(shù)和總數(shù)
The ''yongshu'' (用數(shù)) are the products
The ''zongshu'' (總數(shù)) is the sum .
5. Determine the minimum non-negative solution
So the total amount of rice each farmer sold 24600 ''sheng'' or 246 ''dan'', and the total amount sold is 738 ''dan''.

