[Geometry] Descartes Four Circle Theorem
By: Tao Steven Zheng(鄭濤)
Rene Descartes (1596 - 1650) found the theorem without proof and sent it to Princess Elizabeth of Bohemia in 1643. The theorem was first proven by Jakob Steiner (1796-1863) nearly 200 years later in 1826. In Edo Japan, this theorem first appeared in a sangaku problem from 1796. The theorem was explained in Hashimoto Masataka's book ''Sanpo Tenzan Shogakusho'' (筭法點(diǎn)竄初學(xué)抄) in 1830.
【Problem】
Suppose there are four circles? lying in a plane, such that each circle is mutually tangent to the other three circles. Let the radius of each circle be
. Prove that
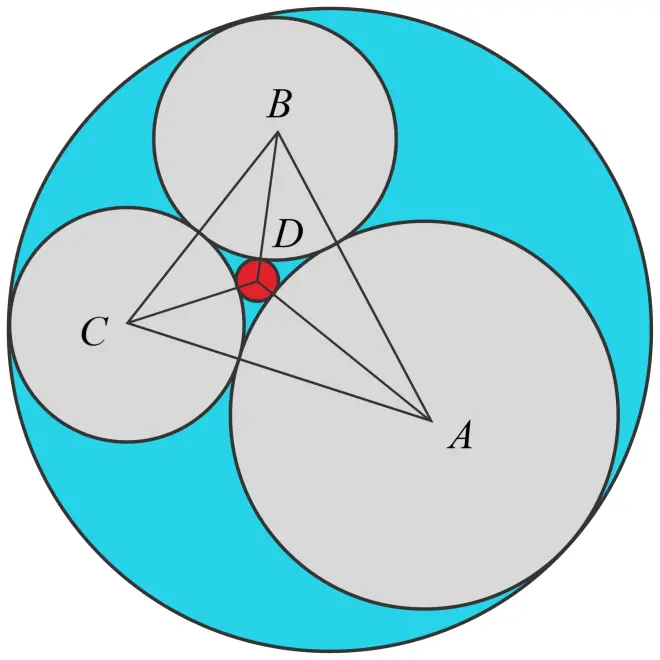
Hint: Given three angles? where
, then
.

【Solution】
Let ,
,
,?
,?
, and
.
?
Furthermore, let there be three angles ,
, and
.
By applying the cosine law on triangle ADB, we get
Expanding each bracket and rearranging yields
Solving for? yields
Using the same method, we can also obtain
Let
Using the trigonometric identity from the hint gives
Expanding and rearranging the above equation yields
Divide both sides of the equation by :
Replace the variables for?? in terms of?
:
Expand the left-hand side of the equation:
Expand the right-hand side of the equation:
Subsequently,
Divide both sides by :
Add? on both sides:
This can be compactly expressed as
Additional Remark
Solving the result for? gives two solutions, one of the incircle (inner circle) and one for the excircle (outer circle).
Incircle radius
Excircle radius

