[Geometry] Prismoidal Formula
By: Tao Steven Zheng (鄭濤)
【Problem】
A ''prismatoid'' is a polyhedron whose vertices all lie in one or the other of two parallel planes. The perpendicular distance between the two planes is called the ''height'' or ''altitude''. The faces that lie in the parallel planes are called the ''bases'' of the prismatoid. The ''midsection'' is the polygon formed by cutting the prismatoid by a plane parallel to the bases halfway between them.
The volume of a prismatoid is given by the “prismoidal formula”:
where is the height,
is the area of the top base,
is
the area of the midsection, and
is the
area of the bottom base.
Use the prismoidal formula to determine the volume of the following solids:
(1) Cube
(2) Paraboloid
(3) Sphere
(4) Bicylinder

【Solution】
(1) Cube
The cube is a square prism. Let the length of each edge be . The area of the top base, midsection and bottom base must all be the same; hence,
.

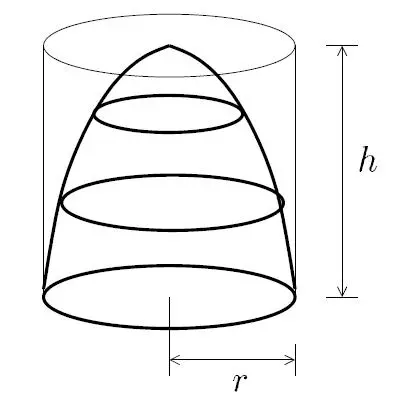
(2) Paraboloid
Let be the height of the paraboloid. The base of a paraboloid is a circle with radius
. The top of the paraboloid is a point with no area. The midsection is harder to determine. From
Volume of a Paraboloid it is found that the radius of a paraboloid as a function of height is
Thus at , the radius of the circle at the midsection is
and the area of the midsection is
.
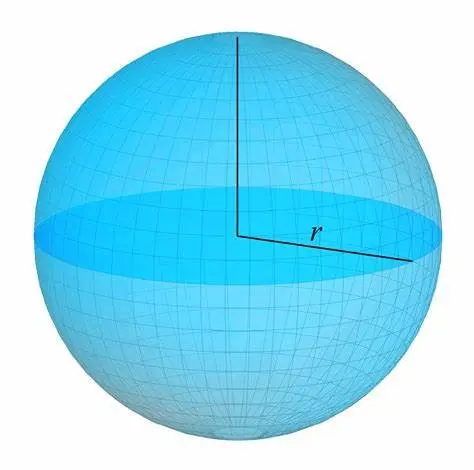
(3) Sphere
Let be the radius of the sphere. The the top base and bottom base of a sphere are points with no area; hence,
. The midsection is a circle with area
.
(4) Bicylinder
The the top and base of the bicylinder are points with no area; hence, . The midsection is a square with area
.


